22. Структура ИС: связи и последовательность вычислений. Принцип избирательности преобразования в ИС.

 

Структуру информационной системы составляет совокупность отдельных ее частей, назы­ваемых подсистемами.

Подсистема — это часть системы, выделенная по какому-либо признаку.

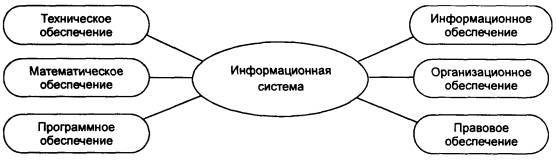
Среди обеспечивающих подсистем обычно выделяют информационное, техническое, математическое, программное, организационное и правовое обеспечение.

 

Информационное обеспечение

Назначение подсистемы информационного обеспечения состоит в своевременном формировании и выдаче достоверной информации для принятия управленческих решений. Главная задача информационной части – сбор, обработка, хранение и выдача необходимой информации.

Принципы:

1)      избирательность в обработке информации используется только часть информации, алгоритмам не нужна вся информация, для одного алгоритма нужна одна информация, для другого другая

2)      целесообразное хранение (сроки хранения)

Определение истинных значений:

По измеренным показаниям определяются остальные значения (все работает в строго определенном диапозоне входных значений)

V_i(t) -> T_i(t)->W_i(t)

Wi(t) = функцияФи(V_i(t))

Wi(t) = a_i + b_iV_i(t)

измеренные значений -> фильтр(интегрирующий(более точный) и экспоненциальный) -> экстраполяция -> интерполяция -> (вроде дифференцирование и интегрирование)

Частотный фильтр: отбрасывает частоты (наверно)

Интегрирующий фильтр 

Экспоненциальный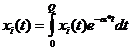

Интерполя́ция — в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений.

Экстраполяция (от экстра… и лат. polio — приглаживаю, выправляю, изменяю) в математике — особый тип аппроксимации (приближения), при котором функция аппроксимируется не между заданными значениями, а вне заданного интервала.

Экстраполяция — приближённое определение значений функции f(x) в точках х, лежащих вне отрезка [х₀, х_n], по её значениям в точках х₀< x₁ < . . . < x_n

Введение

Главной задачей информационной подсистемы, как части общей ИУВС, является сбор, обработка, хранение и выдача информации.

Рассмотрим более подробно особенности реализации информационной системы (ИС), ориентируясь, прежде всего, на задачи последующего управления сложным объектом. Большая часть информации об объекте (в том числе об управляемых и управляющих переменных и контролируемых входах) вводится в ИС автоматически от датчиков, эта информация называется первичной и она поступает в вычислительный комплекс непрерывно, через определенные интервалы времени .

В связи с большими объёмами  информации осуществляется её архивирование и хранение для последующей обработки (создание архивов событий, аварийной сигнализации, изменение технологических параметров во времени, полное или частичное сохранение параметров через определенное время и т.д.). Ясно, что с течением времени работы ИУВС общие объемы хранимой информации будут увеличиваться и необходимо её как можно быстрее обработать и хранить результаты такой обработки, вместо самих исходных данных (кроме, конечно, данных аварийной сигнализации, защиты и блокировки, которые сохраняются за более длительные интервалы времени).

Именно улучшение процессов сбора и обработки информации с использованием ЭВМ послужили основанием для внедрения ИС как первого этапа реализации ИУС в целом. Но и после внедрения даже самых сложных методов и систем управления, сбор и обработка данных необходимы, например, для уточнения модели, совершенствования функционирования системы, управление её эволюцией и т.д. Рассмотрим основные функции, цели и методы обработки информации.

 

Основные функции ИС

Обычно выделяют несколько групп функций, которые представлены ниже.

9.2.1 Сбор и предварительная обработка информации.

9.2.2 Вычисление неизмеряемых (косвенно определяемых величин).

9.2.3  Регистрация и контроль состояния объекта и системы управления в целом.

9.2.4 Визуализация информации для представления ее лицу, принимающему решение – оператору.

9.2.5 Обмен информацией с системой более высокого уровня и/или другими подсистемами ИУВС в целом.

Каждая из этих групп функций, в зависимости от типа объекта и системы управления, разбивается на более подробные (подфункции). Так, например, на уровне 9.1 различают:

– опрос аналоговых и дискретных датчиков с заданным интервалом времени ;

– расчет действительных (истинных) значений параметров;

– фильтрация сигналов от помех;

– централизованный контроль технологических параметров.

В зависимости от типа объекта и системы управления каждая из этих групп функций и подфункций может быть представлена более подробно. Влияет на содержание функций ИС и тот уровень управления, о котором идет речь.

 

Типовые операции предварительной обработки информации

9.3.1. Определение истинных значений измеряемых параметров:

а) масштабирование / линейный случай:

.

Коэффициенты  для каждого канала измерений должны быть заранее известны или определены на этапе настройки системы.

b) нелинейный случай:

.

Такая зависимость имеет место, например, при определении расхода жидкости или газа по перепаду давления.

c) определение истинного значения по переходному процессу при импульсном измерении (так определяют температуру расплава)

Определение истинной температуры проводится по передаточной функции  и ее реакции на ступенчатое воздействие (заштриховано)

 

 

 

 

 

d) получение обобщенных зависимостей для групп датчиков – групповая интерполяционная модель для однотипных датчиков:

 

9.3.2. Интерполяция и экстраполяция показаний датчиков

Речь идет об обработке измерений при дискретном измерении непрерывно изменяющихся величин. Возникает задача восстановления значений измеряемых величин в моменты времени, которые не совпадают с моментами измерений – это интерполяция (экстраполяция) во времени.

Аналогичная задача имеет место при восстановлении информации в некоторых точках пространства (по длине, на плоскости, в объеме) – интерполяция по одной или нескольким пространственным координатам / например, в метеорологических или геологических исследованиях. Наиболее практичными оказались методы статистической интерполяции:

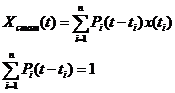
Определение искомых коэффициентов  осуществляется из условия минимизации среднеквадратичной погрешности истинного значения . Обычно число точек n невелико, а при небольшой дискретности достаточно ограничиться двумя-четырьмя точками. При этом должно соблюдаться правило [   ]: время между соседними замерами меньше времени  полного спада корреляционной функции []. Обычно рекомендуют выбор дискретности . Различие погрешности интерполяции и экстраполяции исследовали в [    ] при малом n.

Если погрешности дискретных измерений невелики, или (ими можно пренебречь), используются детерминированные методы, хорошо известные из вычислительной математики, например, интерполяционный полином Ньютона, интерполяционные методы Гаусса, Стерлинга и Бесселя, интерполяционный полином Лагранжа и др. Весьма эффективными методами интерполяции являются сплайн-функции, в частности кубические сплайны. В специальных задачах широко используются полиномы Чебышева, преобразования Фурье[    ].

 

9.3.3. Фильтрация измерений от помех.

Существует обширная литература, посвященная проблемам оптимальной фильтрации сигналов от помех. Более точные фильтры являются и более сложными; их реализация обычно приводит к увеличению объема памяти, занимаемой программой фильтрации, а также к увеличению времени работы УВМ. При построении ИУС число датчиков достигает сотен и тысяч и каждому приходится искать разумный компромисс между погрешностью фильтра и простотой (а значит и экономичностью) его реализации.

Общий подход к проблеме фильтрации был дан Харкевичем А.А. [   ] в простой и понятной форме «метода накопления»: входные сигналы складываются в суммирующем устройстве-накопителе и далее решающее устройство дает ответ ("да" или "нет") на вопрос о наличии сигнала. Отношение сигнал-помеха возрастает в n раз (по сравнению с отсутствием накопления). Этот общий результат распространен как на дискретные фильтры, так и на непрерывные варианты: 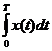 или  и являются частными случаями некоторого общего оптимального метода.

Наиболее часто используемыми на практике простыми методами фильтрации являются:

a) скользящее среднее: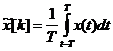  

или в дискретном варианте:

b) экспоненциальное сглаживание, как некоторое рекуррентное соотношение

 

         

или

 

с) общий случай цифрового фильтра:

т.е. мы должны хранить в памяти ЭВМ текущие значения измеренного сигнала x[k], а также оценки входного и выходного сигналов фильтра, полученные на этапах фильтрации. Выбором интервалов хранения данных (n,m) и коэффициентов (a_i,b_j) получают серию вариантов цифровых фильтров, частными случаями которых являются скользящее среднее и экспоненциальный фильтр, рассмотренные выше.

d) возникающее запаздывание в получении оценок  компенсируют построением т.н. прогнозирующих фильтров. В зависимости от требующейся точности различают экстраполяторы 0,1,2,3… порядка, в которых используются экспоненциальные оценки средних 1,2,3 порядков соответственно. Разумеется, соответственно выбираются значения n=1, m=1,2,3 с различными модификациями вычисления коэффициентов <a_i,b_j>.

 

9.4. Альтернативность и модульность

Аналогичным образом могут быть проанализированы и другие функции информационных подсистем:

– контроль состояния и диагностика работоспособности оборудования;

– косвенное измерение, определение неизмеряемых показателей работы оборудования;

– интегрирование расходов перерабатываемых материалов и/или энергетических затрат;

– определение скорости изменения параметров (обычно это необходимо для управляемых величин);

– подготовка данных для управления и вышестоящих систем (включая визуализацию для принятия решения оператором).

Часть из них будет более подробно рассмотрена ниже. Однако принципиально соблюдается подход, сформулированный ранее: одна и та же функция будет реализовываться несколькими алгоритмами (методами, моделями), выбор из возможного множества альтернатив осуществляется с учетом специфики управляемого объекта и технических возможностей вычислительной системы.

 

9.5. Типовые дискретные модули

Вместе с тем, могут быть выделены некоторые типовые модели и алгоритмы, которые из условий практической реализации используются наиболее часто, чтобы ввести их в состав общего программного обеспечения любой ИУС как обязательные. Такие типовые модули в программном обеспечении помогают наиболее быстро осуществить настройку системы, а специфические особенности ИУВС учесть через процедуры построения модулей, которые войдут в состав специального математического и программного обеспечения – СпМО.

Легко видеть, что типовые математические операции в уже рассмотренных задачах этой и предыдущих глав следующие:

– линейные преобразования:

– накопленные суммы:

– приращения на интервале измерения:

– сравнение с порогом:

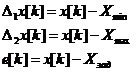
– запоминание текущих и вычисленных оценок на нескольких интервалах времени:

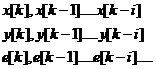
– взвешенные суммы:

;       

– векторные преобразования алгебраического типа:

и операции обращения матриц

– линейные дифференциальные уравнения:

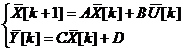
Все эти типовые модули ОМО должны быть соответствующим образом оформлены, чтобы обеспечить удобство их настройки по входным и выходным параметрам.

Существенно при этом для «больших» систем соблюдать принцип избирательности обработки информационных потоков, основной смысл которого заключается в том, что в зависимости от смысла и назначения, каждый сигнал обрабатывается не во всех, а только в части модулей обработки, т.е. имеет свой маршрут, который при компоновке и настройке системы может быть задан своим графом, или в общем случае матрицей связей типовых модулей.

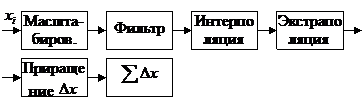Так например, рассмотренная функциональная схема предварительной обработки информации используется не для всех  общего вектора измерений , а только для их части, например:

 

Возможны и более сложные маршруты обработки информационных сигналов (линейные, разветвляющиеся, суммирующееся и т.д.)

Задание таких маршрутов осуществляется не только в пространстве, но и во времени, особенно в системах реального времени.